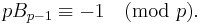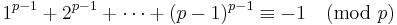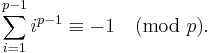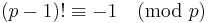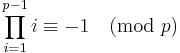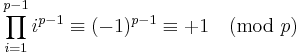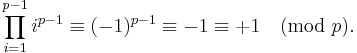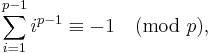Agoh–Giuga conjecture
In number theory the Agoh–Giuga conjecture on the Bernoulli numbers Bk postulates that p is a prime number if and only if
The conjecture as stated is due to Takashi Agoh (1990); an equivalent formulation is due to Giuseppe Giuga, from 1950, to the effect that p is prime iff
which may also be written as
It is trivial to show that p being prime is sufficient for the second equivalence to hold, since if p is prime, Fermat's little theorem states that
for 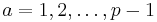 , and the equivalence follows, since
, and the equivalence follows, since 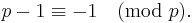
The statement is still a conjecture since it has not yet been proven that if a number n is not prime (that is, n is composite), then the formula does not hold. It has been shown that a composite number n satisfies the formula iff it is both a Carmichael number and a Giuga number, and that if such a number exists, it has at least 13,800 digits (Borwein, Borwein, Borwein, Girgensohn 1996).
The Agoh-Giuga conjecture bears a similarity to Wilson's theorem, which has been proven to be true. Wilson's theorem states that a number p is prime iff
which may also be written as
or, for odd prime p
and, for even prime p=2
So, the truth of the Agoh-Giuga conjecture combined with Wilson's theorem would give: a number p is prime iff
and
References
- Agoh, T, "On Giuga’s conjecture" Manuscripta Math., 87(4), 501–510 (1995).
- Borwein, D.; Borwein, J. M., Borwein, P. B., and Girgensohn, R. "Giuga's Conjecture on Primality", American Mathematical Monthly, 103, 40–50, (1996). pdf
- Giuga, G. "Su una presumibile proprietà caratteristica dei numeri primi", Ist. Lombardo Sci. Lett. Rend. A, 83, 511–528 (1950).